PBS IBL Sepcular

“Yeah It’s on. ”

前言

接上篇PBS IBL Diffuse，这次实现了基于图像的光照specular部分。

IBL SPECULAR PBS效果如下：

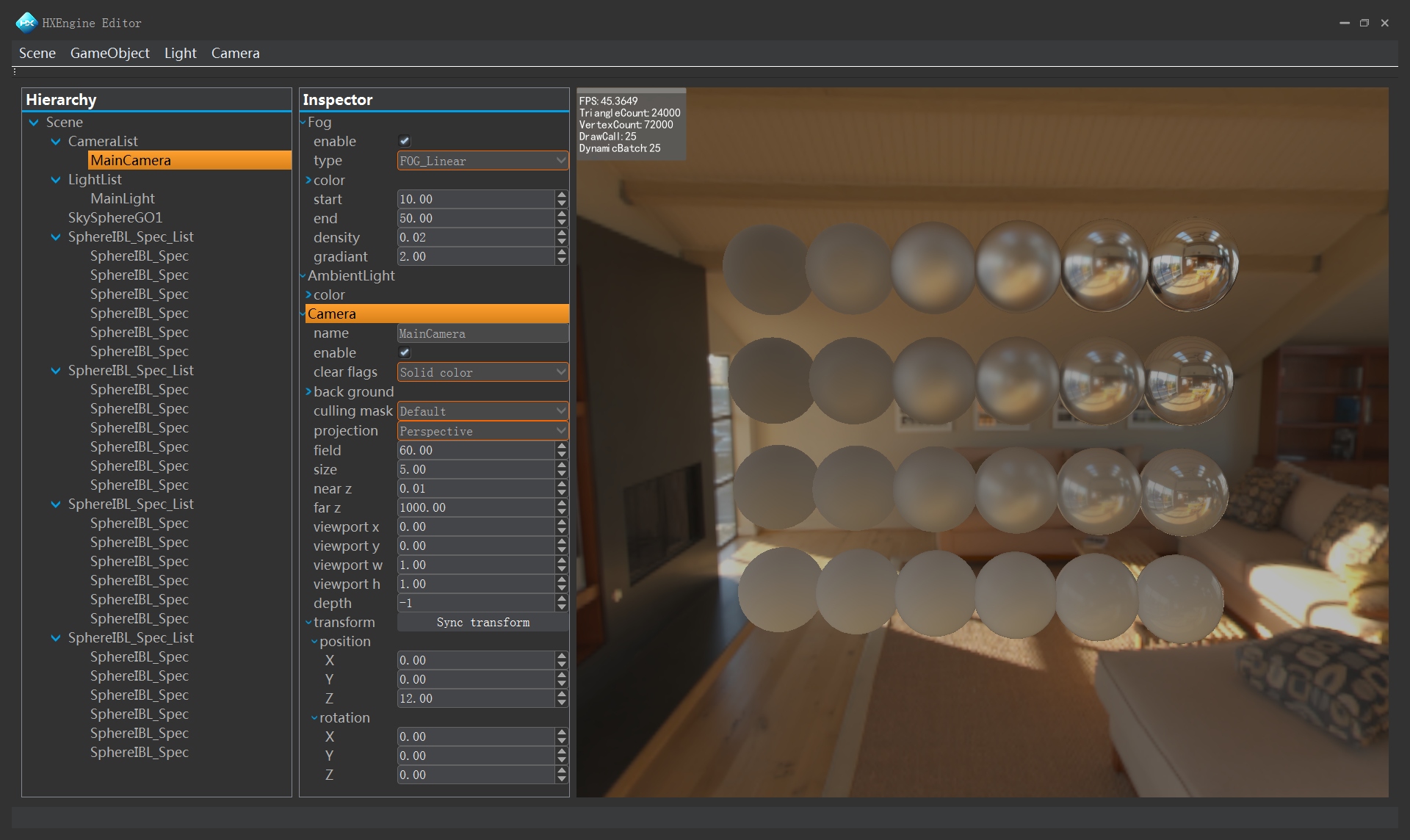
正文

渲染方程

上上篇给出的渲染方程：
$L_o = \int_\Omega (f_d + f_s) L_i (n \cdot w_i){\rm d}w_i$

本篇处理Specular部分：
$L_o=\int_\Omega f_sL_in⋅w_idw_i$
$=\int_\Omega L_i(l)f(l, v)cos\theta dw_i$
通过Importace Sampling，使用Monte Carlo积分来求解上面的积分方程：
$L_0 \approx \frac{1}{N}\sum_{k=1}^{N}\frac{L_i(l_k) f(l_k, v) cos\theta_k}{p(l_k, v)}$
Epic Games将上述公式划分成了两个不同求和部分，这两个不同的求和部分能够分别通过预先计算来得到结果。
$L_0 \approx \frac{1}{N}\sum_{k=1}^{N}\frac{L_i(l_k) f(l_k, v) cos\theta_k}{p(l_k, v)} \approx (\frac{1}{\sum_{k=1}^{N}cos\theta_k}\sum_{k=1}^{N}L_i(l_k) cos\theta_k)(\frac{1}{N}\sum_{k=1}^{N}\frac{f(l_k, v)cos\theta_k}{p(l_k, v)})$
我们分别将上面两个求和部分命名为LD项和DFG项。其中，LD项是对入射光进行求和的部分，需要输入描述周围环境光照的环境贴图；DFG项和光照信息无关，所以只要预计算一次，就能够重复利用了。

预计算过程

主要任务就是将均匀分布转化为重要性分布采样点后求光照信息

利用hammersley算法将采样变量i采样数sampler生成作用域[0，1]的2维均匀分布点
通过PDF求出CDF，用上一步均匀分布点对CDF(累积密度函数)求逆后使用GGX进行采样，得到球面坐标的重要性采样点
利用球面坐标得到半角向量并由切线空间转化到世界空间
利用半角向量和视向量得到光照向量
使用基于重要性的光照向量对环境CubeMap进行采样
采样结果累积最后除以采样数得到该点法线方向半球空间的光照数据保存到卷积CubeMap中

Hammersley低偏差序列：

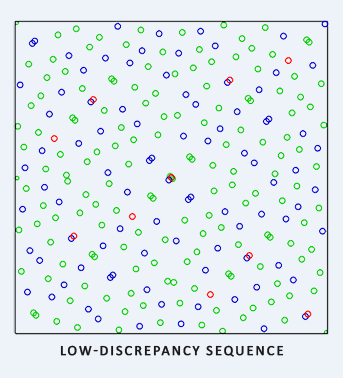
uint sampler = 256u;
vec3 specular = vec3(0.0, 0.0, 0.0);

for (uint i = 0u; i < sampler; i++) {
    vec2 xi = hammersley(i, sampler);
    vec3 h = importance_sampling_ggx(xi, roughness, n);
    vec3 l = 2.0 * dot(v, h) * h - v;

    float ndotv = max(0.0, dot(n, v));
    float ndoth = max(0.0, dot(n, h));
    float vdoth = max(0.0, dot(v, h));
    float ndotl = max(0.0, dot(n, l));

    if (ndotl > 0.0) {
        vec3 light = filtering_cube_map(CubeMap, l).xyz;
        float G = calc_Geometry_Smith_IBL(n, v, l, roughness);
        vec3 F = calc_fresnel(h, v, F0);
        specular = specular + light * F * G * vdoth / (ndoth * ndotv);
    }
}
specular = specular / sampler;

EquirectangularMap转化成CubeMap

参见上篇对应章节，这里使用同样的方式生成。

LD项CubeMap生成

$LD = \frac{1}{\sum_{k=1}^{N}cos\theta_k}\sum_{k=1}^{N}L_i(l_k) cos\theta_k$
对GGX进行Importance Sampling时，Epic Games假定norma = view = reflect向量，这会产生一定偏差。对不同的roughness分别进行预计算，然后将结果保存在LD的CubeMap的不同mipmap level上面。

vec3 convolution_cube_map(samplerCube cube, int faceIndex, vec2 uv) {
    // Calculate tangent space base vector
    vec3 n = calc_normal(faceIndex, uv);
    n = normalize(n);
    vec3 v = n;
    vec3 r = n;

    // Convolution
    uint sampler = 1024u;
    vec3 color = vec3(0.0, 0.0, 0.0);
    float weight = 0.0;
    for (uint i = 0u; i < sampler; i++) {
        vec2 xi = hammersley(i, sampler);
        vec3 h = importance_sampling_ggx(xi, Roughness, n);
        vec3 l = 2.0 * dot(v, h) * h - v;

        float ndotl = max(0, dot(n, l));
        if (ndotl > 0.0) {
            color = color + filtering_cube_map(CubeMap, l).xyz * ndotl;
            weight = weight + ndotl;
        }
    }

    color = color / weight;

    return color;
}

DFG项2DTexture生成

$DFG = \frac{1}{N}\sum_{k=1}^{N}\frac{f(l_k, v)cos\theta_k}{p(l_k, v)}$
其中：
$f(l_k,v) = \frac{DFG}{4(n⋅l)(n⋅v)}$
$p(l_k,v) = \frac{D(n⋅h)}{4(v⋅h)}$
$cos\theta_k = n⋅l$
代入得：
$ DFG=\frac{1}{N}\sum_{k=1}^{N}\frac{f(l_k, v)cos\theta_k}{p(l_k, v)}$
$=\frac{1}{N}\sum_{k=1}^{N}\frac{DFG}{4(n⋅l)(n⋅v)}⋅\frac{4(v⋅h)}{D(n⋅h)}⋅(n⋅l)$
$=\frac{1}{N}\sum_{k=1}^{N}\frac{FG}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}$
$=\frac{1}{N}\sum_{k=1}^{N}\frac{(F0+(1-F0)(1-v⋅h)^5)G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}$
$=\frac{1}{N}\sum_{k=1}^{N}\frac{(F0⋅[1-(1-v⋅h)^5]+(1-v⋅h)^5)G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}$
$=F0⋅[\frac{1}{N}\sum_{k=1}^{N}\frac{([1-(1-v⋅h)^5])G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}]+[\frac{1}{N}\sum_{k=1}^{N}\frac{(1-v⋅h)^5G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}] $
令： $scale = \frac{1}{N}\sum_{k=1}^{N}\frac{([1-(1-v⋅h)^5])G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}$
$bais = \frac{1}{N}\sum_{k=1}^{N}\frac{(1-v⋅h)^5G}{(n⋅v)}⋅\frac{(v⋅h)}{(n⋅h)}$
因此：
$DFG = F0*scale + bias$

通过上面的推导可总结出：
输入：roughness和ndotv
输出：scale和bais
我们使用一张2D贴图来进行保存，其中u坐标表示ndotv，v坐标表示roughness。每一个像素的r表示scale，g表示bias

vec3 convolution_cube_map(vec2 uv) {
    vec3 n = vec3(0.0, 0.0, 1.0);
    float roughness = uv.y;
    float ndotv = uv.x;

    vec3 v = vec3(0.0, 0.0, 0.0);
    v.x = sqrt(1.0 - ndotv * ndotv);
    v.z = ndotv;

    float scalar = 0.0;
    float bias = 0.0;

    // Convolution
    uint sampler = 1024u;
    for (uint i = 0u; i < sampler; i++) {
        vec2 xi = hammersley(i, sampler);
        vec3 h = importance_sampling_ggx(xi, roughness, n);
        vec3 l = 2.0 * dot(v, h) * h - v;

        float ndotl = max(0.0, l.z);
        float ndoth = max(0.0, h.z);
        float vdoth = max(0.0, dot(v, h));

        if (ndotl > 0.0) {
            float G = calc_Geometry_Smith_IBL(n, v, l, roughness);

            float G_vis = G * vdoth / (ndotv * ndoth);
            float Fc = pow(1.0 - vdoth, 5.0);

            scalar = scalar + G_vis * (1.0 - Fc);
            bias = bias + G_vis * Fc;
        }
    }

    vec3 color = vec3(scalar, bias, 0.0);
    color = color / sampler;

    return color;
}

IBL Specular 着色

vec3 calc_ibl(vec3 n, vec3 v, vec3 albedo, float roughness, float metalic) {
    vec3 F0 = mix(vec3(0.04, 0.04, 0.04), albedo, metalic);
    vec3 F = calc_fresnel_roughness(n, v, F0, roughness);

    // Diffuse part
    vec3 T = vec3(1.0, 1.0, 1.0) - F;
    vec3 kD = T * (1.0 - metalic);

    vec3 irradiance = filtering_cube_map(IrradianceMap, n);
    vec3 diffuse = kD * albedo * irradiance;

    // Specular part
    float ndotv = max(0.0, dot(n, v));
    vec3 r = 2.0 * ndotv * n - v;
    vec3 ld = filtering_cube_map_lod(PerfilterEnvMap, r, roughness * 9.0);
    vec2 dfg = textureLod(IntegrateBRDFMap, vec2(ndotv, roughness), 0.0).xy;
    vec3 specular = ld * (F0 * dfg.x + dfg.y);

    return diffuse + specular;
}

后记

所有实现可下载引擎源码进行查看

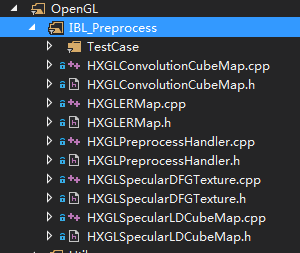
HXGLERMap用于将EquirectangularMap转化成CubeMap
HXGLConvolutionCubeMap对CubeMap进行黎曼和采样，渲染到低分辨率的CubeMap中, IBL diffuse用
HXGLSpecularLDCubeMap对CubeMap进行重要性采样，渲染到带Mipmaps的CubeMap中, IBL specular LD项用
HXGLSpecularDFGTexture生成：输入为roughness和ndotv，输出为scale和bais的2D贴图，IBL specular DFG项用

参考文献

https://learnopengl.com/PBR/IBL/Specular-IBL
Real Shading in Unreal Engine 4

"游戏引擎"

前言

正文