“Yeah It’s on. ”
前言
最近在往引擎中添加基于物理的着色,接上篇直接光照PBS,这次实现了基于图像的光照,此篇介绍diffuse部分的实现。
IBL DIFFUSE PBS效果如下:
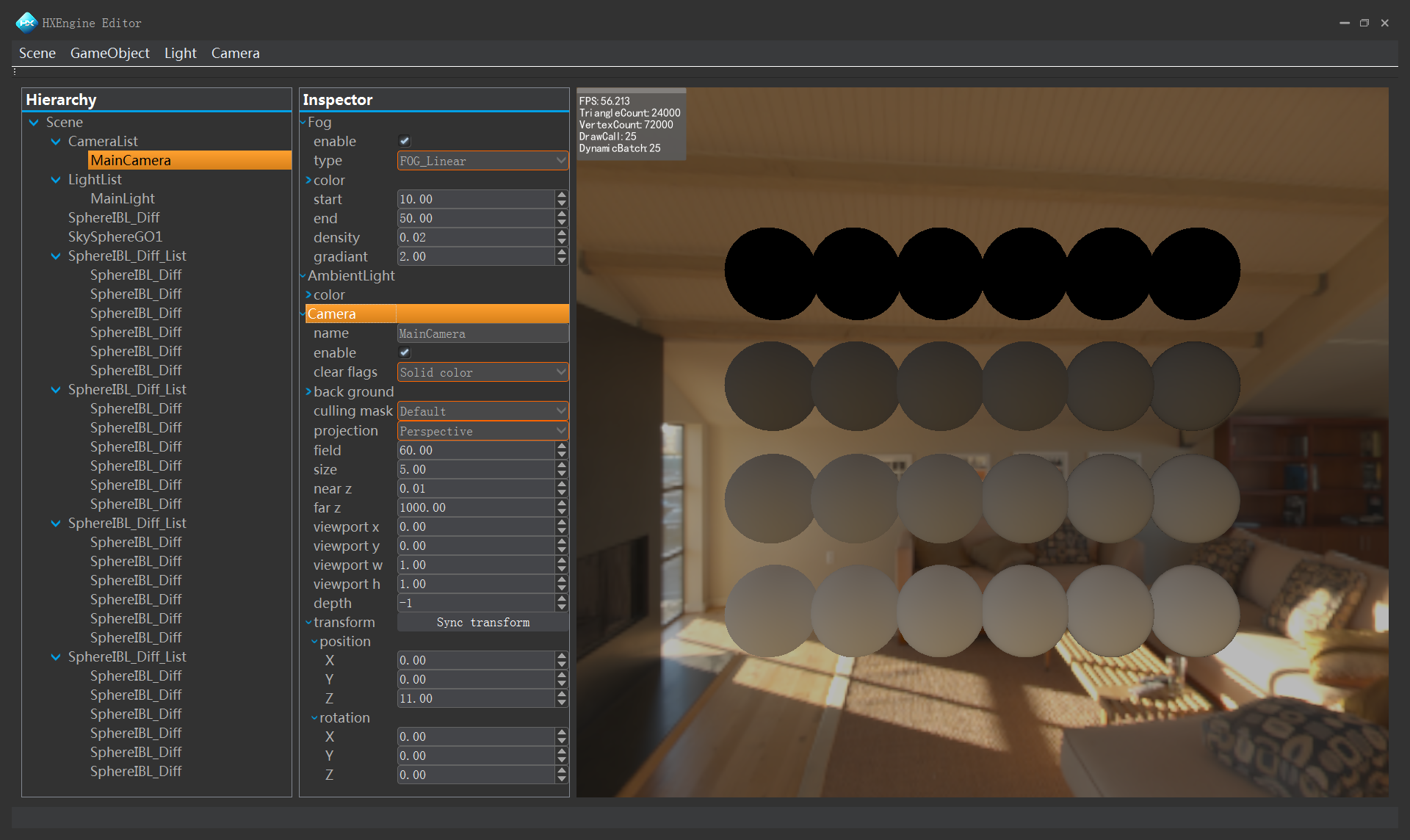
正文
渲染方程
上篇给出的渲染方程:
$L_o = \int_\Omega (f_d + f_s) L_i (n \cdot w_i){\rm d}w_i$
本篇处理漫反射部分:
$L_o=\int_\Omega f_dL_in⋅w_idw_i$
$\int_\Omega \ldots {\rm d}w_i$:这里点pi法线方向上的半球中所有入射光线我们从环境贴图中进行卷积计算获取。
我们可以在sIBL archive下载到丰富的HDRI环境贴图。这个网站里面的HDR贴图并不是CubeMap的形式,而是EquirectangularMap的形式进行保存的,所以首先我们需要将此EquirectangularMap渲染到CubeMap中。
EquirectangularMap转化成CubeMap
.hdr文件可使用github上开源的stb_image库来读取并绑定到GL_TEXTURE_2D上。使用法线转化成UV坐标采样该纹理来绘制球体
vec2 sampling_equirectangular_map(vec3 n)
{
float u = atan(n.z, n.x);
u = (u + PI) / (2.0 * PI);
float v = asin(n.y);
v = (v * 2.0 + PI) / (2.0 * PI);
return vec2(u, v);
}
然后通过设置FOV为90度的摄像机,分别朝着+X,-X,+Y,-Y,+Z,-Z去观察该球体,然后渲染CubeMap的6个面,从而得到一张HDR的CubeMap。

预计算漫反射CubeMap
$L_o=\int_\Omega f_dL_in⋅w_idw_i$
其中:$f_d = kD\frac{c}{\pi}$对于同一点为常量,因此可从积分中提取出来:
$L_o=f_d\int_\Omega L_in⋅w_idw_i$
然后转化为球面坐标系:
$L_o(p,\phi_o, \theta_o) = f_d \int_{\phi = 0}^{2\pi} \int_{\theta = 0}^{\frac{1}{2}\pi} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta$
其中:$n⋅w_i=cos\theta$,$dw_i=sin\theta d\theta d\phi$
然后利用黎曼和将积分简化为求和公式:
$L_o \approx f_d \frac{2\pi}{N_1} \frac{\pi}{2N_2}\sum_0^{N_1} \sum_0^{N_2} L_i cos\theta sin\theta$
其中:
$f_d = kD \frac{c}{\pi}$
代入得:
$L_o \approx kD \frac{c}{\pi} \frac{2\pi}{N_1} \frac{\pi}{2N_2}\sum_0^{N_1} \sum_0^{N_2} L_i cos\theta sin\theta = \frac{kD⋅c⋅\pi}{N_1 N_2} \sum_0^{N_1} \sum_0^{N_2} L_i cos\theta sin\theta$
float samplingStep = 0.025;
int sampler = 0;
vec3 l = vec3(0.0, 0.0, 0.0);
for (float phi = 0.0; phi < 2.0 * PI; phi = phi + samplingStep) {
for (float theta = 0.0; theta < 0.5 * PI; theta = theta + samplingStep) {
vec3 d = calc_cartesian(phi, theta); // Transform spherical coordinate to cartesian coordinate
d = d.x * r + d.y * u + d.z * n; // Transform tangent space coordinate to world space coordinate
l = l + filtering_cube_map(CubeMap, normalize(d)) * cos(theta) * sin(theta); // L * (ndotl) * sin(theta) d(theta)d(phi)
sampler = sampler + 1;
}
}
l = PI * l * (1.0 / sampler);
}
$p_i$点法线半球空间漫反射信息卷积到32*32的低频CubeMap中:

IBL Diffuse 着色
$L_o \approx \frac{kD⋅c⋅\pi}{N_1 N_2} \sum_0^{N_1} \sum_0^{N_2} L_i cos\theta sin\theta$
其中:
$\frac{\pi}{N_1 N_2} \sum_0^{N_1} \sum_0^{N_2} L_i cos\theta sin\theta$
已经通过预计算保存在了Cube Map里面,所以我们只要根据法线n获取Cube Map里面对应的值,然后乘上剩下的kD∗c就可以了
vec3 calc_ibl(vec3 n, vec3 v, vec3 albedo, float roughness, float metalic) {
vec3 F0 = mix(vec3(0.04, 0.04, 0.04), albedo, metalic);
vec3 F = calc_fresnel_roughness(n, v, F0, roughness);
vec3 T = vec3(1.0, 1.0, 1.0) - F;
vec3 kD = T * (1.0 - metalic);
vec3 irradiance = filtering_cube_map(IrradianceMap, n);
return kD * albedo * irradiance;
}
后记
这里涉及到积分运算,《普林斯顿微积分读本》是本不错的这方面的书
参考文献
https://learnopengl.com/PBR/IBL/Diffuse-irradiance
https://en.wikipedia.org/wiki/Riemann_sum