“Yeah It’s on. ”
前言
最近在往引擎中添加基于物理的着色,实现了直接光照部分,后续调整引擎框架实现通用的render texture组件后利用IBL和预计算实现间接光照及性能优化。
直接光照PBS效果如下:
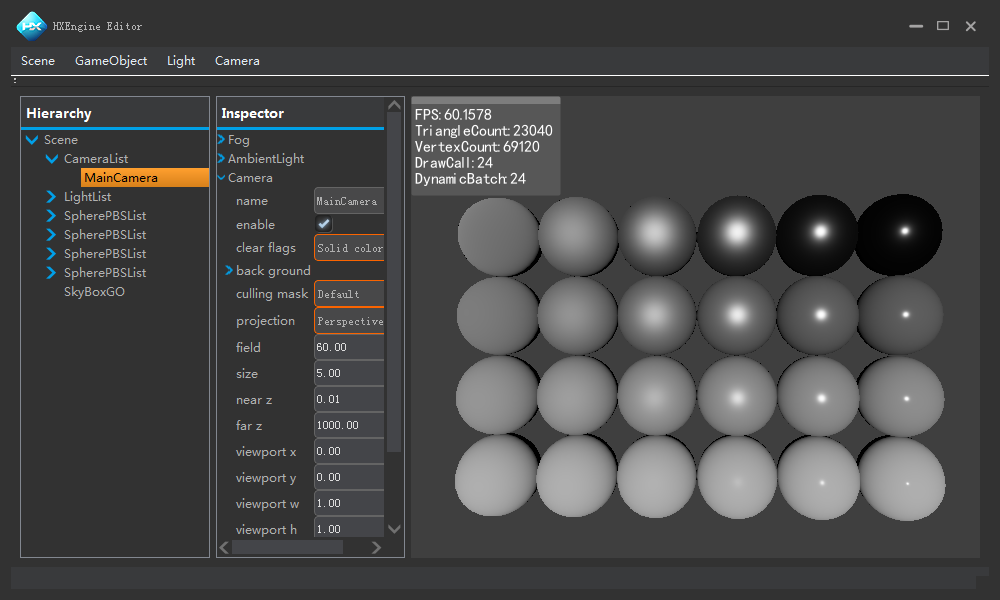
正文
渲染方程
完整的渲染方程:
$L_o = \int_\Omega f(p_i, w_i, w_o) L_i(p_i, w_i) n \cdot w_i{\rm d}w_i$
其中:
$L_o$:表示的是经过着色之后,从$w_o$方向观察点$p_i$时的颜色
$f(p_i, w_i, w_o)$:表示的是点$p_i$上,从$w_o$方向反射出去的光照与从$wi$方向的入射的光照的比值,该函数称为BRDF(Bidirectional Reflection Distribution Function)
$L_i(p_i, w_i)$:表示从$w_i$方向入射到$p_i$点上的光照
$n \cdot w_i$:表示的是光照的反射强度与光照方向与接受光照表面法线方向之间角度的关系,即Lambert Law
$\int_\Omega \ldots {\rm d}w_i$:表示的是在点$p_i$法线方向上的半球,所有入射光线方向的积分
当处理一束光照射到物质表面的时候,可以分成了两个不同的反射部分进行处理,分别是漫反射和镜面反射。所以渲染方程就变成了如下的形式:
$L_o = \int_\Omega (f_d + f_s) L_i (n \cdot w_i){\rm d}w_i$
也就是将原先的BRDF函数分为了两个不同的部分:漫反射部分和镜面反射部分。
直接光照计算时,对于单一解析光源来说(比如平行光,点光源等),物体表面上同一个点只会从一个方向接受到来自光源的光照,所以不需要进行积分计算。对于多个解析光源,我们也只要简单的分别对光源进行上述公式的计算,然后叠加结果即可。 $L_o = (f_d + f_s) L_i(n \cdot w_i)$
漫反射部分
这里使用经典的Lambertian Reflection模型:
$f_d = \frac{c}{\pi}$
镜面反射部分
建立在微表面模型上,这里使用Cook-Torrance模型:
$f_s = \frac{D \cdot F \cdot G}{4 \cdot (n \cdot l)(n \cdot v)}$
其中:
D:表示Normal Distribution Function(NDF)法线分布函数,这里选用GGX函数
$D(n,h,\alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2(\alpha^2-1)+1)^2}$
F:表示Fresnel反射
$F(n,v,F_0) = F_0 + (1 - F_0)(1 - (n \cdot v))^5$
G:表示Geometry Function,又称之为Shadow and Mask项,这里使用Schlick-GGX函数
$G_{SchlickGGX}(n, v, \alpha)=\frac{n \cdot v}{(n \cdot v)(1-k) + k}$
其中$k = \frac{\alpha}{2}$
同时由于G项描述了Shadow和Mask两中情况,所以最终的G项为:
$G(n,v,l,\alpha) = G_{SchlickGGX}(n,v,\alpha) \cdot G_{SchlickGGX}(n,l,\alpha)$
新渲染方程
$L_o = (kd \cdot \frac{c}{\pi} + \frac{D \cdot F \cdot G}{4 \cdot (n \cdot l)(n \cdot v)}) L_i(n \cdot w_i)$
代码实现
#version 330
uniform vec3 Albedo;
uniform float Metalic;
uniform float Roughness;
uniform vec3 eyePos;
in vec3 vs_fs_position;
in vec3 vs_fs_normal;
out vec3 oColor;
const float PI = 3.1415927;
vec3 calc_frenel(vec3 n, vec3 v, vec3 F0)
{
float ndotv = max(dot(n, v), 0.0);
return F0 + (vec3(1.0, 1.0, 1.0) - F0) * pow(1.0 - ndotv, 5.0);
}
float calc_NDF_GGX(vec3 n, vec3 h, float roughness)
{
float a = roughness * roughness;
float a2 = a * a;
float ndoth = max(dot(n, h), 0.0);
float ndoth2 = ndoth * ndoth;
float t = ndoth2 * (a2 - 1.0) + 1.0;
float t2 = t * t;
return a2 / (PI * t2);
}
float calc_Geometry_GGX(float costheta, float roughness)
{
float a = roughness;
float r = a + 1.0;
float r2 = r * r;
float k = r2 / 8.0;
float t = costheta * (1.0 - k) + k;
return costheta / t;
}
float calc_Geometry_Smith(vec3 n, vec3 v, vec3 l, float roughness)
{
float ndotv = max(dot(n, v), 0.0);
float ndotl = max(dot(n, l), 0.0);
float ggx1 = calc_Geometry_GGX(ndotv, roughness);
float ggx2 = calc_Geometry_GGX(ndotl, roughness);
return ggx1 * ggx2;
}
vec3 calc_lighting_direct(vec3 n, vec3 v, vec3 l, vec3 h, vec3 albedo, float roughness, float metalic, vec3 light) {
vec3 F0 = mix(vec3(0.04, 0.04, 0.04), albedo, metalic);
vec3 F = calc_frenel(h, v, F0);
vec3 T = vec3(1.0, 1.0, 1.0) - F;
vec3 kD = T * (1.0 - metalic);
float D = calc_NDF_GGX(n, h, roughness);
float G = calc_Geometry_Smith(n, v, l, roughness);
vec3 Diffuse = kD * albedo * vec3(1.0 / PI, 1.0 / PI, 1.0 / PI);
float t = 4.0 * max(dot(n, v), 0.0) * max(dot(n, l), 0.0) + 0.001;
vec3 Specular = D * F * G * vec3(1.0 / t, 1.0 / t, 1.0 / t);
float ndotl = max(dot(n, l), 0.0);
return (Diffuse + Specular) * light * vec3(ndotl, ndotl, ndotl);
}
void main(void)
{
vec3 view = eyePos - vs_fs_position;
view = normalize(view);
vec3 lightPos = vec3(0.0, 0.0, 200.0);
vec3 light = lightPos - vs_fs_position;
light = normalize(light);
vec3 h = normalize(view + light);
vec3 color = calc_lighting_direct(normalize(vs_fs_normal), view, light, h, Albedo, Roughness, Metalic, vec3(2.5, 2.5, 2.5));
// base tone mapping
color = color / (color + vec3(1.0, 1.0, 1.0));
// gamma correction
color = pow(color, vec3(1.0 / 2.2, 1.0 / 2.2, 1.0 / 2.2));
oColor = color;
}
注:Fresnel效果计算
vec3 F0 = mix(vec3(0.04, 0.04, 0.04), albedo, metalic);
vec3 F = calc_frenel(h, v, F0);
第一段就是计算出合适的$F_0$值出来,如果是非金属材质,那么就使用0.04来表示;如果是金属材质,就是用albedo里面存放的$F_0$属性;如果是介于之间的,就使用金属度进行插值。
注:漫反射比例
由于F项表示的就是镜面反射的比例,那么剩下的就是漫反射的比例,再考虑金属材质没有漫反射部分的情况,得到如下的代码:
vec3 T = vec3(1.0, 1.0, 1.0) - F;
vec3 kD = T * (1.0 - metalic);
后记
引擎集成直接光照的PBR比较简单,只要理解基础理论,一个片元着色器就能搞定。