算法

Algorithm Training

"算法训练"

Posted by A-SHIN on November 3, 2018

“Yeah It’s on. ”

前言

刷题杂记

正文

  • 时间复杂度限定可利用：hashmap等空间换时间、二分法、滑动窗口法
  • 连续子数组相关问题尝试用hashmap[sum-k] or hashmap[sum%k]法>滑动窗口法>建立累加和数组方法>暴力方法
  • DSF用stack，BSF用queue
  • 寻路问题可用DSF，最优解可用DP
  • 钱币找零问题使用贪心算法
  • 背包问题使用动态规划法
  • N皇后问题使用回溯法
一般DFS DP形式：
int DFS(int i, int j, int n , int k, vector<vector<int>>& grid, vector<vector<int>>& dp)
{
	if (dp[i][j] > 0)
	{
		return dp[i][j];
	}
	int left = grid[i][j], right = grid[i][j], up = grid[i][j], down = grid[i][j];
	if (i > k-1 && grid[i- k][j] > grid[i][j])
	{
		left += DFS(i - k, j, n, k, grid, dp);
	}
	if (i < n-k && grid[i+ k][j] > grid[i][j])
	{
		right += DFS(i + k, j, n, k, grid, dp);
	}
	if (j > k-1 && grid[i][j- k] > grid[i][j])
	{
		up += DFS(i, j - k, n, k, grid, dp);
	}
	if (j < n-k && grid[i][j+ k] > grid[i][j])
	{
		down += DFS(i, j + k, n, k, grid, dp);
	}
	dp[i][j] = max(max(left, right), max(up, down));
	return dp[i][j];
}
总结深度优先与广度优先的区别（转）
1、 区别

1） 二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

2） 深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：

  • 先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树
  • 中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。
  • 后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

      广度优先遍历：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。　

3） 深度优先搜素算法：不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。
      广度优先搜索算法：保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快。
      通常 深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。
所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。
      广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。
但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

2、 二叉树的遍历

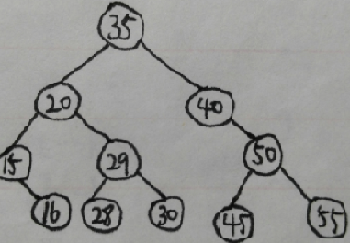
先序遍历（递归）：35 20 15 16 29 28 30 40 50 45 55
中序遍历（递归）：15 16 20 28 29 30 35 40 45 50 55
后序遍历（递归）：16 15 28 30 29 20 45 55 50 40 35
先序遍历（非递归）：35 20 15 16 29 28 30 40 50 45 55
中序遍历（非递归）：15 16 20 28 29 30 35 40 45 50 55
后序遍历（非递归）：16 15 28 30 29 20 45 55 50 40 35
广度优先遍历：35 20 40 15 29 50 16 28 30 45 55

代码：

package BinaryTreeTraverseTest;  
  
import java.util.LinkedList;  
import java.util.Queue;  
  
/** 
 * 二叉树的深度优先遍历和广度优先遍历 
 * @author Fantasy 
 * @version 1.0 2016/10/05 - 2016/10/07 
 */  
public class BinaryTreeTraverseTest {  
    public static void main(String[] args) {  
          
    BinarySortTree<Integer> tree = new BinarySortTree<Integer>();  
          
        tree.insertNode(35);  
        tree.insertNode(20);  
        tree.insertNode(15);  
        tree.insertNode(16);  
        tree.insertNode(29);  
        tree.insertNode(28);  
        tree.insertNode(30);  
        tree.insertNode(40);  
        tree.insertNode(50);  
        tree.insertNode(45);  
        tree.insertNode(55);  
          
        System.out.print("先序遍历（递归）：");  
        tree.preOrderTraverse(tree.getRoot());  
        System.out.println();  
        System.out.print("中序遍历（递归）：");  
        tree.inOrderTraverse(tree.getRoot());  
        System.out.println();  
        System.out.print("后序遍历（递归）：");  
        tree.postOrderTraverse(tree.getRoot());  
        System.out.println();  
          
        System.out.print("先序遍历（非递归）：");  
        tree.preOrderTraverseNoRecursion(tree.getRoot());  
        System.out.println();  
        System.out.print("中序遍历（非递归）：");  
        tree.inOrderTraverseNoRecursion(tree.getRoot());  
        System.out.println();  
        System.out.print("后序遍历（非递归）：");  
        tree.postOrderTraverseNoRecursion(tree.getRoot());  
        System.out.println();  
          
        System.out.print("广度优先遍历：");  
        tree.breadthFirstTraverse(tree.getRoot());  
    }  
}  
  
/** 
 * 结点 
 */  
class Node<E extends Comparable<E>> {  
      
    E value;  
    Node<E> left;  
    Node<E> right;  
      
    Node(E value) {  
        this.value = value;  
        left = null;  
        right = null;  
    }  
      
}  
  
/** 
 * 使用一个先序序列构建一棵二叉排序树（又称二叉查找树） 
 */  
class BinarySortTree<E extends Comparable<E>> {  
      
    private Node<E> root;  
      
    BinarySortTree() {  
        root = null;  
    }  
      
    public void insertNode(E value) {     
        if (root == null) {  
            root = new Node<E>(value);  
            return;  
        }      
        Node<E> currentNode = root;  
        while (true) {  
            if (value.compareTo(currentNode.value) > 0) {  
                if (currentNode.right == null) {  
                    currentNode.right = new Node<E>(value);  
                    break;  
                }  
                currentNode = currentNode.right;  
            } else {  
                if (currentNode.left == null) {  
                    currentNode.left = new Node<E>(value);  
                    break;  
                }  
                currentNode = currentNode.left;  
            }  
        }  
    }  
      
    public Node<E> getRoot(){  
        return root;  
    }  
  
    /** 
     * 先序遍历二叉树（递归） 
     * @param node 
     */  
    public void preOrderTraverse(Node<E> node) {  
        System.out.print(node.value + " ");  
        if (node.left != null)  
            preOrderTraverse(node.left);  
        if (node.right != null)  
            preOrderTraverse(node.right);  
    }  
      
    /** 
     * 中序遍历二叉树（递归） 
     * @param node 
     */  
    public void inOrderTraverse(Node<E> node) {  
        if (node.left != null)  
            inOrderTraverse(node.left);  
        System.out.print(node.value + " ");  
        if (node.right != null)  
            inOrderTraverse(node.right);  
    }  
      
    /** 
     * 后序遍历二叉树（递归） 
     * @param node 
     */  
    public void postOrderTraverse(Node<E> node) {  
        if (node.left != null)  
            postOrderTraverse(node.left);  
        if (node.right != null)  
            postOrderTraverse(node.right);  
        System.out.print(node.value + " ");  
    }  
      
    /** 
     * 先序遍历二叉树（非递归） 
     * @param root 
     */  
    public void preOrderTraverseNoRecursion(Node<E> root) {  
        LinkedList<Node<E>> stack = new LinkedList<Node<E>>();  
        Node<E> currentNode = null;  
        stack.push(root);  
        while (!stack.isEmpty()) {  
            currentNode = stack.pop();  
            System.out.print(currentNode.value + " ");  
            if (currentNode.right != null)  
                stack.push(currentNode.right);  
            if (currentNode.left != null)  
                stack.push(currentNode.left);  
        }  
    }  
      
    /** 
     * 中序遍历二叉树（非递归） 
     * @param root 
     */  
    public void inOrderTraverseNoRecursion(Node<E> root) {  
        LinkedList<Node<E>> stack = new LinkedList<Node<E>>();  
        Node<E> currentNode = root;  
        while (currentNode != null || !stack.isEmpty()) {  
            // 一直循环到二叉排序树最左端的叶子结点（currentNode是null）  
            while (currentNode != null) {  
                stack.push(currentNode);  
                currentNode = currentNode.left;  
            }  
            currentNode = stack.pop();  
            System.out.print(currentNode.value + " ");  
            currentNode = currentNode.right;  
        }     
    }  
      
    /** 
     * 后序遍历二叉树（非递归） 
     * @param root 
     */  
    public void postOrderTraverseNoRecursion(Node<E> root) {  
        LinkedList<Node<E>> stack = new LinkedList<Node<E>>();  
        Node<E> currentNode = root;  
        Node<E> rightNode = null;  
        while (currentNode != null || !stack.isEmpty()) {  
            // 一直循环到二叉排序树最左端的叶子结点（currentNode是null）  
            while (currentNode != null) {  
                stack.push(currentNode);  
                currentNode = currentNode.left;  
            }  
            currentNode = stack.pop();  
            // 当前结点没有右结点或上一个结点（已经输出的结点）是当前结点的右结点，则输出当前结点  
            while (currentNode.right == null || currentNode.right == rightNode) {  
                System.out.print(currentNode.value + " ");  
                rightNode = currentNode;  
                if (stack.isEmpty()) {  
                    return; //root以输出，则遍历结束  
                }  
                currentNode = stack.pop();  
            }  
            stack.push(currentNode); //还有右结点没有遍历  
            currentNode = currentNode.right;  
        }  
    }  
      
    /** 
     * 广度优先遍历二叉树，又称层次遍历二叉树 
     * @param node 
     */  
    public void breadthFirstTraverse(Node<E> root) {  
        Queue<Node<E>> queue = new LinkedList<Node<E>>();  
        Node<E> currentNode = null;  
        queue.offer(root);  
        while (!queue.isEmpty()) {  
            currentNode = queue.poll();  
            System.out.print(currentNode.value + " ");  
            if (currentNode.left != null)  
                queue.offer(currentNode.left);  
            if (currentNode.right != null)  
                queue.offer(currentNode.right);  
        }  
    }  
      
}
3、 图

图的遍历之 深度优先搜索和广度优先搜索

后记

二叉搜索树使用中序遍历、深度优先(用递归简单，用stack中序后序比较复杂)

CATALOG
    FEATURED TAGS
    技术 杂记
    FRIENDS